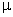 , точности решения задачи
, точности решения задачи 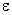 , а также две матрицы начальных предельных
максимальных и минимальных значений координат оптимизируемых векторов
популяции.
, а также две матрицы начальных предельных
максимальных и минимальных значений координат оптимизируемых векторов
популяции.
Модифицированный генетический алгоритм (МГА) содержит в себе генетические качества статистической селекции групп родительских особей на десятичном уровне. Для исключения неудачных потомков при их генерировании МГА реализована процедура регулярного поиска локальных экстремумов. Для регулярного поиска использованы операции метода деформируемого многогранника. Стратегия МГА ориентирована на поиск локальных экстремумов и наилучшего из них. При достаточно размере популяции (числа пробных решений) МГА с высокой вероятностью находит глобальный экстремум.
В первом блоке алгоритма вводится размерность задачи оптимизации
N,число особей в популяции 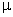 , точности решения задачи
, точности решения задачи 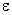 , а также две матрицы начальных предельных
максимальных и минимальных значений координат оптимизируемых векторов
популяции.
, а также две матрицы начальных предельных
максимальных и минимальных значений координат оптимизируемых векторов
популяции.
В первом пункте блока 2 создается матрица случайных чисел для координат 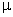 начальных векторов оптимизации X n. Для ее создания может быть использована функция-генератор
случайных, равномерно распределенных на интервале от 0 до
начальных векторов оптимизации X n. Для ее создания может быть использована функция-генератор
случайных, равномерно распределенных на интервале от 0 до
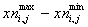 чисел
чисел
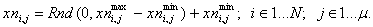 |
(1) |
Такие функции имеются практически во всех программных средах.
Во втором пункте блока 2 для матрицы координат векторов начальной популяции вычисляются значения функции цели
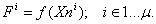 |
(2) |
Функция цели может быть задана в аналитическом виде или ее значения могут быть вычисленными алгоритмически программой.
В третьем пункте блока 2 производится объединение матрицы X n и вектора F, создается матрица состояния популяции X
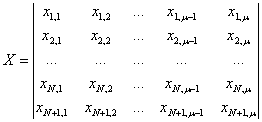 |
(3) |
Матрица X в процессе генетического отбора обновляется от поколения к поколению и является показателем степени приближения решения к наилучшему или глобальному экстремуму.
В третьем блоке производится сортировка столбцов матрицы X по возрастанию элементов N+1 строки. После сортировки последние столбцы матрицы X будут содержать неперспективные особи, которые при смене поколения популяций должны быть элиминированы, т.е. заменены на новые, более перспективные. Коэффициент элиминирования принят равным 0,1.
В четвертом блоке популяция оценивается на вырожденность матрицы состояния X . Если условия блока 4 выполняются, задача считается решенной и алгоритм выходит на окончание расчета и в блоке 5 выводится первый столбец матрицы X.
В противном случае в блоке 5 устанавливается начальное значение счетчика поколений r=0 и алгоритм переходит к блоку 7.
В первом пункте блока 7 создается вектор N+1 целых случайных чисел P.
Случайные числа выбираются из интервала от 1 до 0,9*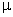 (по числу оставшихся в популяции перспективных особей). Вектор P так же, как и в (1) может быть получен из встроенной функции
Rnd(…) с выделением целых частей из генерируемых вещественных чисел
(по числу оставшихся в популяции перспективных особей). Вектор P так же, как и в (1) может быть получен из встроенной функции
Rnd(…) с выделением целых частей из генерируемых вещественных чисел
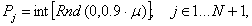 |
(4) |
Во втором пункте блока 7 из матрицы состояния X выбираются столбцы родительской группы N+1 особей для r-го регулярного поиска потомка. Принцип формирования матрицы родительской группы A n показан ниже
 |
(5) |
В третьем пункте блока 7 вычисляются N+1 элементов вектора значений функции цели Fr для столбцов матрицы A n , а в четвертом создается матрица состояния родительской группы особей r-го регулярного поиска локального экстремума А. Элементами N+1 строки матрицы А является вектор значений функции цели Fr
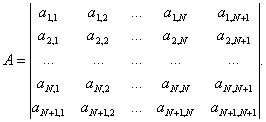 |
(6) |
В блоке 8 производится сортировка столбцов матрицы А по возрастанию N+1 строки, а в блоке 9 оценивается степень сжатия
столбцов матрицы А. Оценка делается по элементам N+1 строки. Если условие блока 9 выполняется, то считается, что локальный
экстремум найден и в блоке 10 первый столбец матрицы А записывается в int( 0,9*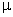 )+r-ый
столбец матрицы X и устанавливается новое значение счетчика поколений r=r+1. Затем, в блоке 11 проверяется число
найденных локальных экстремумов r.
)+r-ый
столбец матрицы X и устанавливается новое значение счетчика поколений r=r+1. Затем, в блоке 11 проверяется число
найденных локальных экстремумов r.
Если выполняется условие
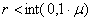 |
(7) |
Если условие (7) не выполняется, то алгоритм переходит ко второй части блок-схемы к блокам регулярного поиска локального экстремума.
В блоке 12 вычисляются координаты центра тяжести матрицы А. Центр тяжести вычисляется без N+1 -го наихудшего столбца. Там же, во втором пункте выполняется операция «отражения» от наихудшего столбца и вычисляется значение функции цели для отраженного N+2-го столбца.
Если значение функции цели в отраженной точке aN+1,N+3 меньше или равно, чем наилучшее aN+1,1, то в блоке 14 выполняется операция «растяжения» матрицы в перспективном направлении. Для нового aN+1,N+4 столбца вычисляется функция цели и сравнивается с наилучшим значением aN+1,1. Если aN+1,N+4 < aN+1,1, то столбец матрицы AN+4 записывается на место наихудшего столбца AN+1 и алгоритм возвращается к блоку 8 для новой сортировки столбцов матрицы А. В противном случае в столбец AN+1 записываются элементы столбца AN+3 и алгоритм переходит к блоку 8.
Если в блоке 13 aN+1,N+3 > aN+1,1, то в блоке 18 элемент aN+1,N+3 сравнивается с элементом aN+1,N, второго после наихудшего столбца. Если aN+1,N+3 < aN+1,N , то в столбец AN+1 записываются элементы столбца AN+3 и алгоритм переходит к блоку 8. В противном случае функция цели в N+3 столбце сравнивается с наихудшим N+1 значением.
Если aN+1,N+3 < aN+1,N+1 , то в столбец AN+1 записываются элементы столбца AN+3 и алгоритм переходит к блоку 20. В противном случае алгоритм переходит к блоку 20 без передачи элементов столбцов.
В блоке 20 выполняется операция «сжатия» матрицы A в пространстве между центром тяжести и наихудшим столбцом и, соответственно, вычисление функции цели в новом N+5 столбце. Если aN+1,N+5 < aN+1,N+1, то в блоке 22 в столбец AN+1 записываются элементы столбца AN+5 и алгоритм переходит к блоку 8. В противном случае в блоке 23 происходит «редукция» матрицы А. Редукция – это уменьшение вдвое расстояния всех столбцов от наилучшего столбца A1. Для новых значений элементов первых N строк всех столбцов матрицы А вычисляются и записываются в N+1 строку значения функции цели. Затем алгоритм переходит к блоку 8.